剪枝&稀疏约束
剪枝作为一种经典技术,已经被广泛运用到各种算法的后处理中。通过剪枝,在减少模型复杂度的同时,还能有效防止过拟合,提高泛化性。
一般而言,剪枝的分类可以从粒度和衡量方式上区分。粒度上有:连接层面和滤波器层面(通道层面);衡量方式上有:权值和输出,而后者一般称为数据驱动的剪枝。
连接层面的剪枝存在的一个普遍的缺点就是:权值分布不具有局部相关性(稀疏矩阵),因此会导致实际的加速效果难以达到理论加速效果。如果想要达到理论上的加速比,那么就需要专门编写的运行库深圳相应的硬件设备,这制约了该方法的通用性。
滤波器层面的剪枝则能很好地保留原有的权值结构(直接丢弃整个滤波器),但是由于保留的滤波器本身存在冗余,因此理论上其剪枝效果(对性能影响)并不如连接层面的精细。
权值衡量的剪枝,是指直接利用权值来衡量连接或者滤波器的重要性,对于连接层面的剪枝,往往是通过权值的大小来衡量;而对于滤波器层面的剪枝,则常常使用\(L_1\)和\(L_2\)来衡量。这种衡量方式,往往是基于权值小的连接或者滤波器对网络贡献程度相对较小的假设,但是却与网络的输出没有直接的关系。一般而言,小权值对损失函数也会起到重要的影响,当压缩率较大的时候,直接剪除这些权值会造成不可逆的严重影响。
数据驱动的剪枝相比之下,则是更加合理的选择。一般而言,这种剪枝也是与滤波器层面剪枝相适应的,因为很难计算某一连接对后续输出的影响。其主要思想是,如果一个滤波器的输出接近零,那么这个滤波器便是冗余可以移除的。
常用的剪枝算法一般有如下操作流程:
- 衡量神经元的重要程度
- 移除一部分不重要的神经元
- 对网络进行微调(fine-tuning)
- 返回第一步,进行下一轮剪枝。
在实际操作中,还常常使用\(L_1\)和\(L_2\)进行稀疏约束(正则化),以促使网络的权重趋向于零,提高剪枝效果。
相关研究
连接层面的权值衡量剪枝:
文献"Learning both weights and connections for efficient neural network."[1]
直接将低于某个阈值的权值连接全部剪除。如果某个连接的权值过低,则表示该连接并不重要,因而可以移除。之后进行fine-tuning以完成参数更新。如此反复,直到剪枝后的网络在性能和规模上达到较好的平衡。他们在保持网络分类精度不下降的情况下将参数数量减少了9~10倍。不过,该方法的一个问题就是,剪枝后的权值分布不具有局部连续性(稀疏矩阵),因此会导致cache和主存之间的频繁切换,从而实际的加速效果无法达到理论的加速效果。
文献"Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding."[1]
基于上一篇文章,为了解决剪枝带来的矩阵稀疏问题,提出了使用常见的稀疏矩阵存储方式:compressed sparse row(CSR)或者compressed sparse column(CSC)来解决。
滤波器层面的权值衡量剪枝:
文献"Pruning Filters for Efficient ConvNets"[2]
计算每个滤波器权值绝对值之和,用来衡量滤波器重要程度。
滤波器层面的数据驱动剪枝:
文献"Channel pruning for accelerating very deep neural networks."[3]和文献"Thinet: A filter level pruning method for deep neural network compression."[4]
提出的方法都非常相近,均是粒度为filter-level的剪枝方法,区别则是文献[3]使用LASSO进行稀疏约束后剪枝,而文献[4]则使用贪婪算法进行剪枝。
文献3
文献4
文献"Learning Efficient Convolutional Networks through Network Slimming"[5]
非常巧妙地利用了Batch Normalization层中的\(γ\)放缩因子来衡量滤波器的重要程度。Batch Normalization的算法如下:

paper5_BN
可以发现,\(γ\)影响着滤波器输出结果\(x_i\)(每个通道对应的feature map)对后续网络输出。因此,对应\(γ\)值比较小的滤波器,可以直接移除(反正乘上\(γ\)后输出都会变的比较小)。作者在训练过程中对\(γ\)加入了LASSO进行稀疏约束,从而使得较小的\(γ\)值压缩到0。另一个比较有意思的feature就是,作者认为这样的衡量方式是具有全局比较性的,也就是说,无需逐层进行层内比较后剪枝再微调。只需一次的全局剪枝后微调即可。而这大大降低了剪枝这种方法的繁琐性。个人认为这篇文献具有很好的参考价值。
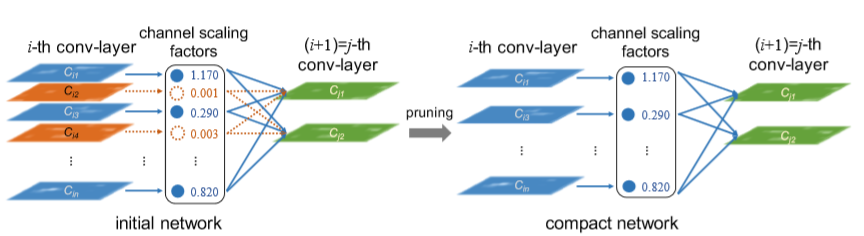
paper5_process
作者还提出了循环迭代剪枝的方式,能够将压缩比例达到非常低的程度。
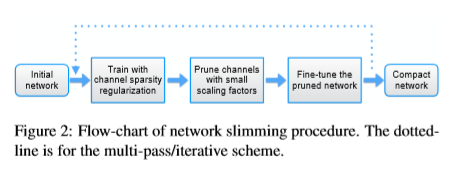
paper5_multi_pass
实验结果如下图:
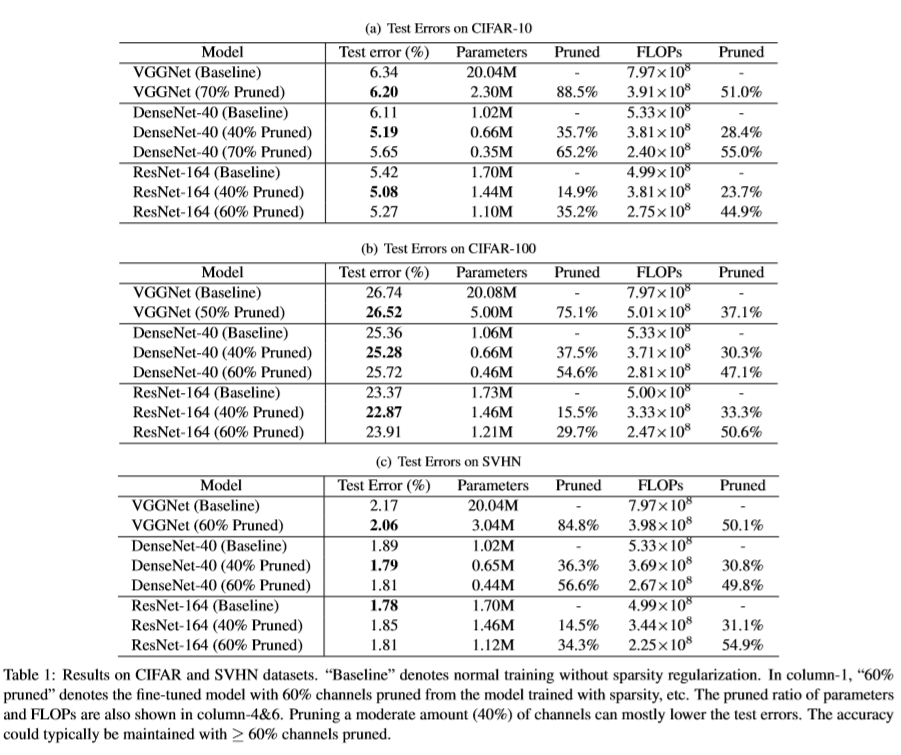
paper5_result
重复迭代的结果如下:
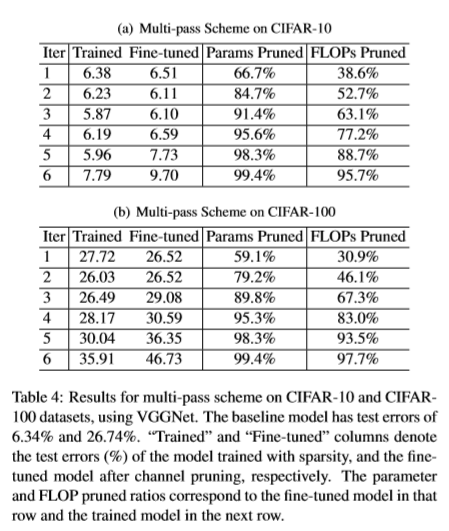
paper5_multi_pass_result
文献"Rethinking the Smaller-Norm-Less-Informative Assumption in Channel Pruning of Convolution Layers"[6]
是一篇有意思的,对剪枝方法中一些关于稀疏约束带来的缺陷进行思考的文章(思考部分没怎么看明白)。文章提出的剪枝方法基于文献[5],主要不同的是,作者不再使用传统的稀疏约束方式,而是使用了一种名为ISTA的稀疏约束方法。
以下是该文章的算法:

paper6_algorithm
实验结果如下图:
cifar10:
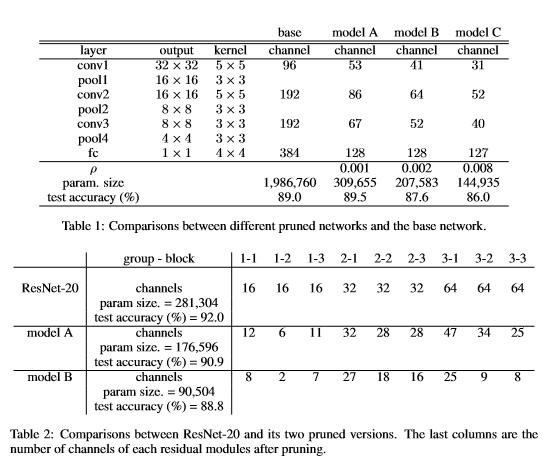
paper6_result1
ILSVRC2012:
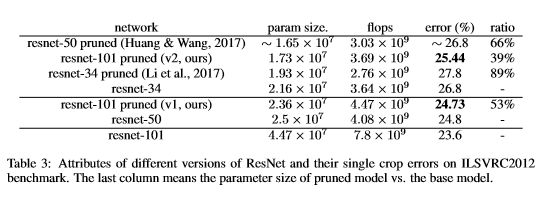
paper6_result2