参数量化
所谓“量化”,指的是降低表达权值所需要的位数。本质是将多个权值映射到同一个数值,从而实现权值共享,降低存储开销。 核心思路:从权值中归纳出若干“代表”,由这些“代表”来表示某一类权重的具体数值。“代表”被存储在码本(codebook)中,而原权值矩阵仅需记录各自的码表索引即可,从而极大地降低了存储开销。
一般而言,可以分为非结构化的标量量化和结构化的向量量化。
相关研究
标量量化
文献"Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding."[1]
这篇文章在量化之前还使用了剪枝的方法(基于作者在另一篇文章中提出的,"Learning both weights and connections for efficient neural network."[1])。是一篇很好的具有启发性的模型综合压缩的文章。最后还提出了使用霍夫曼编码进行更进一步的压缩。过程如下图:
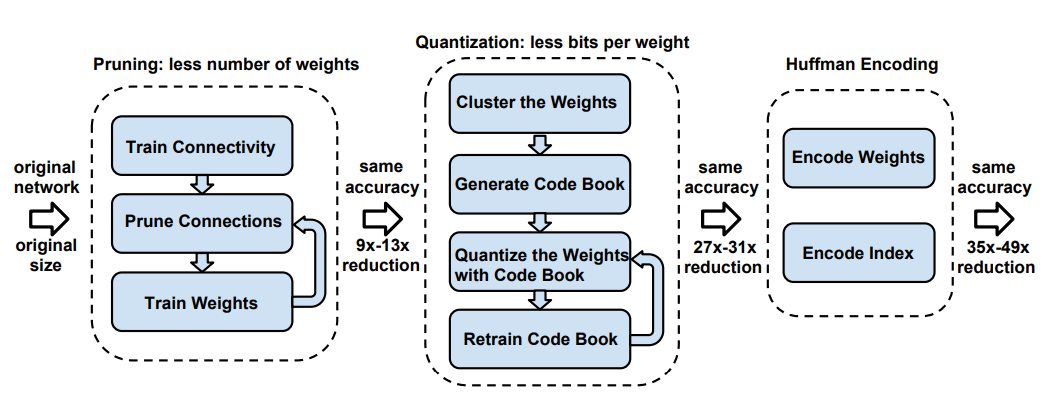
paper1_process
文中提出了一种量化方法,对于每个权值矩阵\(W∈R^{m×n}\),首先将其展平为向量形式\(w∈R^{1×mn}\),然后对这\(mn\)个权值进行k-means聚类:
\(\arg min_c \sum_{i}^{mn} \sum_{j}^{k} \|W_i-c_j\|_2^2\)
这样一来,只需将\(k\)个聚类中心保存在码本中即可(仅需\(log_2^k\)bits)。该方法能够将权值矩阵的存储空间降低为原来的\(\frac{mnb}{mnlog_2^k + kb}\),其中\(b\)为存储原始权值所需要的比特位数。在网络性能损失不大的情况下,能够将模型大小减少8到16倍。不足之处在于,当压缩比率比较大时,分类精度会大幅下降。
为了解决量化带来的精度降低,作者利用每个权值回传的梯度对当前的码本进行更新,具体为:将同一个类的权值回传的梯度相加,作为聚类中心的的梯度,然后进行更新。如下图:
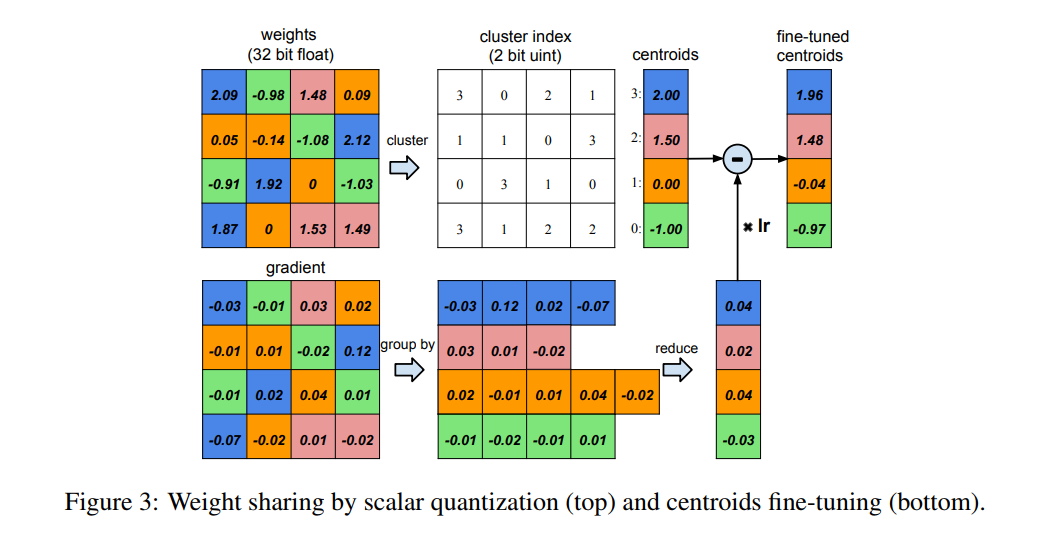
paper1_backward_update
实验结果:
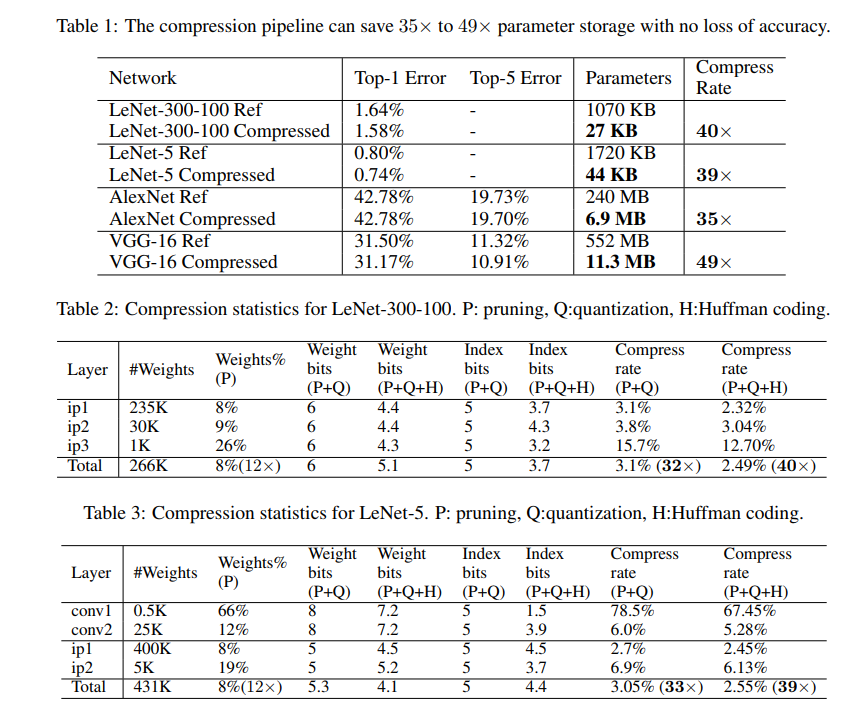
paper1_result1
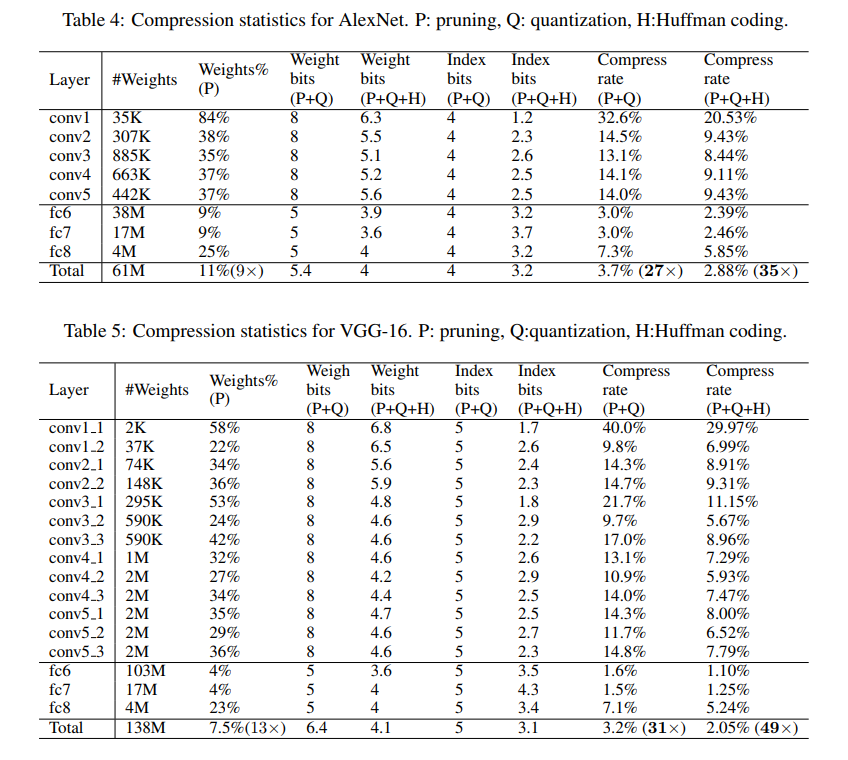
paper1_result2
向量量化
一种方法是乘积量化,基本思路是,先将权值矩阵划分为若干(\(s\))个不相交的子矩阵,然后依次对每个子矩阵进行聚类。之后执行标量量化的过程。向量量化考虑了更多的空间结构信息,具有更高的精度和鲁棒性,但是由于码本中存储的是向量,因此其压缩率为\((32mn)/(32knlog_2^{kms})\)